Simpangan rata-rata, Simpangan Baku, Varian
Sekumpulan data kuantitatif yang tidak dikelompokkan dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukan simpangan rata-rata (SR) dengan menggunakan rumus :
dan juga rumus
Contoh Soal 1 :
Hitung simpangan rata-rata dari data kuantitatif berikut :
12, 3, 11, 3, 4, 7, 5, 11
Pembahasan :
Jadi, simpangan rata-ratanya adalah 3,25.
Contoh Soal 2 :
Hitunglah simpangan rata-rata nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka seperti Tabel 1.
Tabel 1. Nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka
Interval Kelas
|
Frekuensi
|
40 – 44
|
3
|
45 – 49
|
4
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
2
|
90 – 94
|
2
|
Penyelesaian :
Kelas
Interval
|
Nilai Tengah (xi)
|
fi
|
|x – x|
|
fi |x – x|
|
40 – 44
|
42
|
3
|
23,7
|
71,1
|
45 – 49
|
47
|
4
|
18,7
|
74,8
|
50 – 54
|
52
|
6
|
13,7
|
82,2
|
55 – 59
|
57
|
8
|
8,7
|
69,6
|
60 – 64
|
62
|
10
|
3,7
|
37
|
65 – 69
|
67
|
11
|
1,3
|
14,3
|
70 – 74
|
72
|
15
|
6,3
|
94,5
|
75 – 79
|
77
|
6
|
11,3
|
67,8
|
80 – 84
|
82
|
4
|
16,3
|
65,2
|
85 – 89
|
87
|
2
|
21,3
|
42,6
|
90 – 94
|
92
|
2
|
26,3
|
52,6
|
Σfi = 71
|
Σfi |x – x| = 671,7
|
Jadi, simpangan rata-rata (SR) = 671,7 / 71 = 9,46.
Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn. Dari data tersebut, dapat diperoleh nilai simpangan baku (S) yang ditentukan oleh rumus berikut.
Contoh Soal 3 :
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Kunci Jawaban :
Jadi, simpangan bakunya adalah 5,83.
Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh x1, x2, …, xn dan masing-masing data mempunyai frekuensi f1, f2, …, fn. Simpangan baku (S) dari data tersebut diperoleh dengan menggunakan rumus :
Contoh Soal 4 :
Hitunglah simpangan baku dari nilai ulangan Fisika dari 71 siswa kelas XI SMA Merdeka sesuai Tabel 1.
Jawaban :
Dari hasil perhitungan sebelumnya diperoleh µ = 65,7.
xi
|
fi
|
xi - µ
|
(xi - µ)2
|
Σfi (xi - µ)2
|
42
|
3
|
–23,7
|
561,69
|
1.685,07
|
47
|
4
|
–18,7
|
349,69
|
1.398,76
|
52
|
6
|
–13,7
|
187,69
|
1.126,14
|
57
|
8
|
– 8,7
|
75,69
|
605,52
|
62
|
10
|
–3,7
|
13,69
|
136,9
|
67
|
11
|
1,3
|
1,69
|
18,59
|
72
|
15
|
6,3
|
39,69
|
595,35
|
77
|
6
|
11,3
|
127,69
|
766,14
|
82
|
4
|
16,3
|
265,69
|
1.062,76
|
87
|
2
|
21,3
|
453,69
|
907,38
|
92
|
2
|
26,3
|
691,69
|
1.383,38
|
Σfi = 60
|
Σfi (xi - µ)2 = 9.685,99
|
Jadi, simpangan bakunya σ :
c. Variansi (Ragam)
Untuk data yang tidak dikelompokkan ataupun data yang dikelompokkan, diperoleh nilai variansi (v) dengan
menggunakan rumus:
Contoh Soal 5 :
Hitunglah variansi dari data Contoh 3.
Pembahasan :
Dari hasil perhitungan Contoh 3. diperoleh S = 5,83 maka :
v = S2 = (5,83)2 = 33,99.
Sumber : http://perpustakaancyber.blogspot.com/2013/04/rumus-simpangan-baku-simpangan-rata-rata-ragam-variansi-koefien-keragaman-contoh-soal-jawaban-statistik-matematika.html


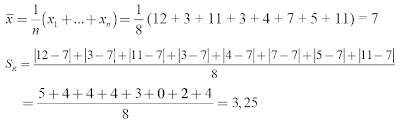












Terima Kasih atas penjelasannya
BalasHapuswah contoh yg simpangan baku untuk tinggi badan ngaco itu.
BalasHapusBukannya standar deviasi = akar kuadrat dari varian ?
BalasHapusIni soal un bukan?
BalasHapus